Теория подобия
Теория подобия- есть обобщение опыта
 Многообразие материального мира требует применения самых разнообразных способов его изучения. Многообразие материального мира требует применения самых разнообразных способов его изучения.
Одним из основных приемов разработки общих теоретических положений является обобщение. Обобщение – есть средство перехода от познания частных явлений к познанию общих. Оно заключается в исследовании таких свойств и явлений материального мира, которые характеризуют не единичное явление, а целый класс однородных в данном отношении явлений. Обобщение имеет огромное значение в теории подобия для выделения из класса однородных явлений группы подобных между собой явлений. Изучив одно из подобных явлений, результаты исследования можно распространить на всю группу подобных явлений
Теория подобия – есть учение о методах научного обобщения эксперимента. Она отвечает на вопрос, как нужно поставить опыт и обработать полученные данные, чтобы их можно было распространить на все подобные явления. Всякое явление природы представляет собой систему материальных тел, которая за счет протекания в ней различных процессов претерпевает определенное изменение состояния. Подобными явлениями называют системы тел, геометрически подобные друг другу, в которых протекают процессы одинаковой физической природы и в которых одноименные величины, характеризующие явления, относятся между собой как постоянные числа.
Теория подобия Материал из Википедии — свободной энциклопедии
. Теория подобия — метод математического моделирования, основанный на переходе от обычных физических величин, влияющих на моделируемую систему, к обобщённым величинам комплексного типа, составленным из исходных физических величин, но в определённых сочетаниях, зависящих от конкретной природы исследуемого процесса. Комплексный характер этих величин имеет глубокий физический смысл отражения взаимодействия различных влияний. 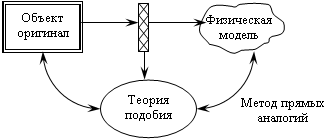 Теория подобия изучает методы построения и применения этих переменных и применяется в тех случаях математического моделирования, когда аналитическое решение математических задач моделирования невозможно из-за сложности и требований к точности. Теория подобия изучает методы построения и применения этих переменных и применяется в тех случаях математического моделирования, когда аналитическое решение математических задач моделирования невозможно из-за сложности и требований к точности.
Теория подобия применяется в этих случаях для синтеза соотношений, получаемых на основе физического механизма изучаемого процесса и данных численного решения или эксперимента.
Анализ размерности
Материал из Википедии — свободной энциклопедии
Не следует путать с теорией размерности — разделом топологии.
Анализ размерности (англ. Dimensional analysis — «размерный анализ» или «пространственное изучение»; чаще говорят «соображения размерности» или «метрические соображения») — инструмент, используемый в физике, химии, технике и нескольких направлениях экономики для построения обоснованных гипотез о взаимосвязи различных параметров сложной системы. Неоднократно применялся физиками на интуитивном уровне не позже XIX века.
Утверждается, что анализ размерностей впервые методически изложен Н. А. Морозовым в монографии «Основы качественного физико-математического анализа и новые физические факторы, обнаруживаемые им в различных явлениях природы» (1908), однако ранее аналогичные методики использовались другими учёными ещё в XIX веке и получили широкую известность после работ Рэлея (около 1892 г.) и Э. Бакингема (π-теорема). Суть метода в простейшем случае заключается в том, что для поиска выражения одного из параметров исследуемой системы через другие из последних составляется формула (их произведение в каких-то степенях), имеющая нужную размерность; часто именно она и оказывается искомым соотношением (с точностью до безразмерного множителя).
Примеры Физика и техника
Простейший пример: если обозначить размерности физической величины буквами M, L, T, и поставить им в соответствие массу, расстояние, время, то такая физическая величина, как скорость, может быть представлена как «расстояние / время», то есть как (L/T), а сила может быть представлена как «масса × ускорение» или «масса × расстояние/время²» или (ML/T²). С помощью таких же соотношений можно выразить мощность, импульс и другие величины, в том числе весьма необычные, такие, как «вязкость» или «скорость переноса мощности» Выбор той или иной системы базовых размерностей не сводится к математике, а определяется физикой задачи.
После выбора системы размерностей необходимо определить величины, характерные для системы (характерные величины). Например, размеры шара могут быть охарактеризованы его радиусом, а размеры кругового цилиндра — двумя величинами (естествен выбор радиуса цилиндра и его длины, но в некоторых задачах может быть удобна пара диаметр-объем или иной набор величин). Характерность величины связана не только с физическими свойствами системы, но и с интересующими нас вопросами. Например, для определения площади земельного участка важно знать какие-либо величины, характеризующие размер, а отражающие свойства не релевантны этой задаче. Однако если вопрос состоит в определении температуры у поверхности, то альбедо земли, наряду со многими другими величинами, является существенным параметром, в то время как размер участка не важен. Из выбранных характерных величин составляются все независимые комбинации, дающие размерность интересующей нас величины.
В простых случаях возможна лишь одна такая комбинация (например, если известен радиус 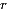 шара и его масса шара и его масса 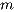 , а интересует плотность материала , а интересует плотность материала 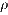 , то существует лишь одна возможная комбинация исходных величин, совпадающая с искомой по размерности: , то существует лишь одна возможная комбинация исходных величин, совпадающая с искомой по размерности: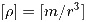 . .
В более сложных задачах комбинаций может быть несколько. Иногда требуется найти не скалярную величину, а функцию (например, распределение скорости жидкости в трубе). В таких случаях наряду с анализом размерностей необходимо учитывать дополнительные физические соображения.
|
| Категория: Математика знает больше, чем физика. | Добавил: Никс (05.12.2016)
|
| Просмотров: 511
| Рейтинг: 0.0/0 |
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] |