Первоначально идея о необходимости расширения понятия действительного числа возникла в результате формального решения квадратных и кубических уравнений, в которых в формулах для корней уравнения под знаком корня стояло отрицательное число. В дальнейшем возникшая теория функций комплексного переменного нашла применение для решения многих задач во всех областях математики и физики.
История
Впервые, по-видимому, мнимые величины были упомянуты в известном труде «Великое искусство, или об алгебраических правилах» Кардано (1545), в рамках формального решения задачи по вычислению двух чисел, которые в сумме дают 10, а при перемножении дают 40. Он получил для этой задачи квадратное уравнение для одного из слагаемых, и нашёл его корни: 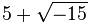 и и 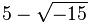 . В комментарии к решению он написал: «эти сложнейшие величины бесполезны, хотя и весьма хитроумны» и «Арифметические соображения становятся все более неуловимыми, достигая предела столь же утонченного, сколь и бесполезного». Возможность использования мнимых величин при решении кубического уравнения, в так называемом неприводимом случае (когда вещественные корни многочлена выражаются через кубические корни из мнимых величин), впервые описал Бомбелли (1572). Он же впервые описал правила сложения, вычитания, умножения и деления комплексных чисел, однако всё равно считал их бесполезной и хитроумной «выдумкой». Выражения, представимые в виде . В комментарии к решению он написал: «эти сложнейшие величины бесполезны, хотя и весьма хитроумны» и «Арифметические соображения становятся все более неуловимыми, достигая предела столь же утонченного, сколь и бесполезного». Возможность использования мнимых величин при решении кубического уравнения, в так называемом неприводимом случае (когда вещественные корни многочлена выражаются через кубические корни из мнимых величин), впервые описал Бомбелли (1572). Он же впервые описал правила сложения, вычитания, умножения и деления комплексных чисел, однако всё равно считал их бесполезной и хитроумной «выдумкой». Выражения, представимые в виде 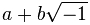 , появляющиеся при решении квадратных и кубических уравнений, стали называть «мнимыми» в XVI—XVII веках с подачи Декарта, который называл их так, отвергая их реальность, и для многих других крупных ученых XVII века природа и право на существование мнимых величин представлялись весьма сомнительными, так же как сомнительными в то время считали и иррациональные числа, и даже отрицательные величины. Лейбниц, например, писал: «Дух божий нашёл тончайшую отдушину в этом чуде анализа, уроде из мира идей, двойственной сущности, находящейся между бытием и небытием, которую мы называем мнимым корнем из отрицательной единицы». Несмотря на это, математики смело применяли формальные методы алгебры вещественных величин и к комплексным, получали корректные вещественные результаты даже из промежуточных комплексных, и это не могло не начать внушать доверие. Долгое время было неясно, все ли операции над комплексными числами приводят к комплексным или вещественным результатам, или, например, извлечение корня может привести к открытию ещё какого-то нового типа чисел. Задача о выражении корней степени из данного числа была решена в работах Муавра (1707) и Котса (1722). Символ для обозначения мнимой единицы предложил Эйлер (1777, опубл. 1794), взявший для этого первую букву слова лат. imaginarius — мнимый. Он же распространил все стандартные функции, включая логарифм, на комплексную область. Эйлер также высказал в 1751 году мысль об алгебраической замкнутости поля комплексных чисел. К такому же выводу пришёл д’Аламбер (1747), но первое строгое доказательство этого факта принадлежит Гауссу (1799). Гаусс и ввёл в широкое употребление термин «комплексное число» в 1831 году, хотя этот термин ранее использовал в том же смысле французский математик Лазар Карно в 1803 году. Арифметическая (стандартная) модель комплексных чисел как пар вещественных чисел была построена Гамильтоном (1837); это доказало непротиворечивость их свойств. , появляющиеся при решении квадратных и кубических уравнений, стали называть «мнимыми» в XVI—XVII веках с подачи Декарта, который называл их так, отвергая их реальность, и для многих других крупных ученых XVII века природа и право на существование мнимых величин представлялись весьма сомнительными, так же как сомнительными в то время считали и иррациональные числа, и даже отрицательные величины. Лейбниц, например, писал: «Дух божий нашёл тончайшую отдушину в этом чуде анализа, уроде из мира идей, двойственной сущности, находящейся между бытием и небытием, которую мы называем мнимым корнем из отрицательной единицы». Несмотря на это, математики смело применяли формальные методы алгебры вещественных величин и к комплексным, получали корректные вещественные результаты даже из промежуточных комплексных, и это не могло не начать внушать доверие. Долгое время было неясно, все ли операции над комплексными числами приводят к комплексным или вещественным результатам, или, например, извлечение корня может привести к открытию ещё какого-то нового типа чисел. Задача о выражении корней степени из данного числа была решена в работах Муавра (1707) и Котса (1722). Символ для обозначения мнимой единицы предложил Эйлер (1777, опубл. 1794), взявший для этого первую букву слова лат. imaginarius — мнимый. Он же распространил все стандартные функции, включая логарифм, на комплексную область. Эйлер также высказал в 1751 году мысль об алгебраической замкнутости поля комплексных чисел. К такому же выводу пришёл д’Аламбер (1747), но первое строгое доказательство этого факта принадлежит Гауссу (1799). Гаусс и ввёл в широкое употребление термин «комплексное число» в 1831 году, хотя этот термин ранее использовал в том же смысле французский математик Лазар Карно в 1803 году. Арифметическая (стандартная) модель комплексных чисел как пар вещественных чисел была построена Гамильтоном (1837); это доказало непротиворечивость их свойств.
Существенно ранее, в 1685 году в работе «Алгебра» Валлис (Англия) показал, что комплексные корни квадратного уравнения с вещественными коэффициентами можно представить геометрически, точками на плоскости. Но это прошло незамеченным. Следующий раз геометрическое истолкование комплексных чисел и действий над ними появилось в работе Весселя (1799). Современное геометрическое представление, иногда называемое «диаграммой Аргана», вошло в обиход после опубликования в 1806-м и 1814-м годах работы Ж. Р. Аргана, повторявшей независимо выводы Весселя. Термины «модуль», «аргумент» и «сопряжённое число» ввёл Коши. Таким образом было обнаружено, что комплексные числа пригодны и для выполнения чисто алгебраических операций сложения, вычитания, умножения и деления векторов на плоскости, что сильно изменило векторную алгебру. В развитие этого подхода начались поиски способа аналогично представить и вектора в трёхмерном пространстве. В результате пятнадцатилетних поисков, в 1843 году Гамильтон предложил обобщение комплексных чисел — кватернионы, которые он был вынужден сделать не трёхмерными, а четырёхмерными; также ему пришлось отказаться от коммутативности операции умножения. Позднее, в 1919 году, стало понятно, что и комплексные числа из вещественных, и кватернионы из комплексных чисел могут быть получены единой процедурой удвоения размерности, так же известной как Процедура Кэли — Диксона. Дальнейшим применением этой процедуры образуются числа, описанные Артуром Кэли в 1845 году, до обнаружения этой процедуры, и названные «Числа Кэли» (октонионы, октавы). Числа, получаемые следующим применением процедуры названы Седенионы. Несмотря на то, что эту процедуру можно повторять и далее, дальнейшие числа названий пока не имеют.
Весь математический материал статьи
|